Chapter 3 Record Linkage
Joshua Tokle and Stefan Bender
As we mentioned in the last chapter, it is often necessary to combine data from multiple sources to get a complete picture of the activities of interest. In addition to just linking data to get additional information, we are also concerned about issues of missing links, duplicative links, and erroneous links. This chapter provides an overview of traditional rule-based and probabilistic approaches, as well as the modern approaches to record linkage using machine learning.
3.1 Motivation
New sources of data offer social scientists great opportunities to bring together many different types of data, from many different sources. Merging different data sets provides new ways of creating population frames that are generated from the digital traces of human activity rather than, say, tax records. These opportunities, however, create different kinds of challenges from those posed by survey data. Combining information from different sources about an individual, business, or geographic entity means that the social scientist must determine whether or not two entities in two different data sources are the same. This determination is not always easy.
We regularly run into situations where we need to combine data from different agencies about the same people to understand future employment or health outcomes for people on social service benefits or those who have recently been released from prison. In the UMETRICS data for example, if data are to be used to measure the impact of research grants, is David A. Miller from Stanford, CA, the same as David Andrew Miller from Fairhaven, NJ, in a list of inventors? Is IBM the same as Big Blue if the productivity and growth of R&D-intensive firms is to be studied? Or, more generally, is individual A the same person as the one who appears on a list that has been compiled? Does the product that a customer is searching for match the products that business B has for sale?
The consequences of poor record linkage decisions can be substantial. In the business arena, Christen reports that as much as 12% of business revenues are lost due to bad linkages (Christen 2012b). In the security arena, failure to match travelers to a “known terrorist” list may result in those individuals entering the country, while overzealous matching could lead to numbers of innocent citizens being detained. In finance, incorrectly detecting a legitimate purchase as a fraudulent one annoys the customer, but failing to identify a thief will lead to credit card losses. Less dramatically, in the scientific arena when studying patenting behavior, if it is decided that two inventors are the same person, when in fact they are not, then records will be incorrectly grouped together and one researcher’s productivity will be overstated. Conversely, if the records for one inventor are believed to correspond to multiple individuals, then that inventor’s productivity will be understated.
This chapter discusses current approaches to joining multiple data sets together—commonly called record linkage.14
We draw heavily here on work by Winkler, Scheuren, and Christen, in particular (Herzog, Scheuren, and Winkler 2007; Christen 2012a; Christen 2012b). To ground ideas, we use examples from a recent paper examining the effects of different algorithms on studies of patent productivity (Ventura, Nugent, and Fuchs 2015).
In addition to the worked examples in this chapter here are a few other papers that show the wide variety of projects using combining records from different sources.15
Glennon (2019) used a unique matched firm-level dataset of H-1B visas and multinational firm activity show that restrictions on H-1B immigration caused increases in foreign affiliate employment. Restrictions also caused increases in foreign patenting, suggesting that there was also a change in the location of innovative activity.
Rodolfa et al. (2020) use machine learning based record linkage to link data about the same individuals together from a criminal justice case management system to help the Los Angeles City Attorney’s office develop individually-tailored social service interventions in a fair and equitable manner. Because the system lacked a global unique person-level identifier, case-level defendant data was used to link cases belonging to the same person using first and last name, date of birth, address, driver’s license number (where available), and California Information and Identification (CII) number (where available).
The National Center for Health Statistics (NCHS) (2019) links the data from the National Health Interview Survey (NHIS) to records from the Social Security Administration, the Centers for Medicare & Medicaid Services, and the National Death Index to investigate the relationship between health and sociodemographic information reported in the surveys and medical care costs, future use of medical services and mortality.
3.2 Introduction to record linkage
There are many reasons to link data sets. Linking to existing data sources to solve a measurement need instead of implementing a new survey results in cost savings (and almost certainly time savings as well) and reduced burden on potential survey respondents. For some research questions (e.g., a survey of the reasons for death of a longitudinal cohort of individuals) a new survey may not be possible. In the case of administrative data or other automatically generated data, the sample size is much greater than would be possible from a survey.
Record linkage can be used to compensate for data quality issues. If a large number of observations for a particular field are missing, it may be possible to link to another data source to fill in the missing values. For example, survey respondents might not want to share a sensitive datum like income. If the researcher has access to an official administrative list with income data, then those values can be used to supplement the survey (Abowd, Stinson, and Benedetto 2006).
Record linkage is often used to create new longitudinal data sets by linking the same entities over time (Jarmin and Miranda 2002). More generally, linking separate data sources makes it possible to create a combined data set that is richer in coverage and measurement than any of the individual data sources (Abowd, Haltiwanger, and Lane 2004).
Example: The Administrative Data Research Network
The UK’s Administrative Data Research Network16 (ADRN) is a major investment by the United Kingdom to “improve our knowledge and understanding of the society we live in … [and] provide a sound base for policymakers to decide how to tackle a range of complex social, economic and environmental issues” by linking administrative data from a variety of sources, such as health agencies, court records, and tax records in a confidential environment for approved researchers. The linkages are done by trusted third-party providers. (Economic and Social Research Council 2016)
Linking is straightforward if each entity has a corresponding unique identifier that appears in the data sets to be linked. For example, two lists of US employees may both contain Social Security numbers. When a unique identifier exists in the data or can be created, no special techniques are necessary to join the data sets.
If there is no unique identifier available, then the task of identifying unique entities is challenging. One instead relies on fields that only partially identify the entity, like names, addresses, or dates of birth. The problem is further complicated by poor data quality and duplicate records, issues well attested in the record linkage literature (Christen 2012a) and sure to become more important in the context of big data. Data quality issues include input errors (typos, misspellings, truncation, extraneous letters, abbreviations, and missing values) as well as differences in the way variables are coded between the two data sets (age versus date of birth, for example). In addition to record linkage algorithms, we will discuss different data preprocessing steps that are necessary first steps for the best results in record linkage.
To find all possible links between two data sets it would be necessary to compare each record of the first data set with each record of the second data set. The computational complexity of this grows quadratically with the size of the data—an important consideration, especially with large amounts of data. To compensate for this complexity, the standard second step in record linkage, after preprocessing, is indexing or blocking, which uses some set of heuristics to create subsets of similar records and reduces the total number of comparisons.
The outcome of the matching step is a set of predicted links—record pairs that are likely to correspond to the same entity. After these are produced, the final stage of the record linkage process is to evaluate the result and estimate the resulting error rates. Unlike other areas of application for predictive algorithms, ground truth or gold standard data sets are rarely available. The only way to create a reliable truth data set sometimes is through an expensive human review process that may not be viable for a given application. Instead, error rates must be estimated.
An input data set may contribute to the linked data in a variety of ways, such as increasing coverage, expanding understanding of the measurement or mismeasurement of underlying latent variables, or adding new variables to the combined data set. It is therefore important to develop a well-specified reason for linking the data sets, and to specify a loss function to proxy the cost of false negative matches versus false positive matches that can be used to guide match decisions. It is also important to understand the coverage of the different data sets being linked because differences in coverage may result in bias in the linked data. For example, consider the problem of linking Twitter data to a sample-based survey—elderly adults and very young children are unlikely to use Twitter and so the set of records in the linked data set will have a youth bias, even if the original sample was representative of the population. It is also essential to engage in critical thinking about what latent variables are being captured by the measures in the different data sets—an “occupational classification” in a survey data set may be very different from a “job title” in an administrative record or a “current position” in LinkedIn data.17
Example: Employment and earnings outcomes of doctoral recipients
A recent paper in Science matched UMETRICS data on doctoral recipients to Census data on earnings and employment outcomes. The authors note that some 20% of the doctoral recipients are not matched for several reasons: (i) the recipient does not have a job in the US, either for family reasons or because he/she goes back to his/her home country; (ii) he/she starts up a business rather than choosing employment; or (iii) it is not possible to uniquely match him/her to a Census Bureau record. They correctly note that there may be biases introduced in case (iii), because Asian names are more likely duplicated and harder to uniquely match (Zolas et al. 2015). Improving the linkage algorithm would increase the estimate of the effects of investments in research and the result would be more accurate.
Comparing the kinds of heterogeneous records associated with big data is a new challenge for social scientists, who have traditionally used a technique first developed in the 1960s to apply computers to the problem of medical record linkage. There is a reason why this approach has survived: it has been highly successful in linking survey data to administrative data, and efficient implementations of this algorithm can be applied at the big data scale. However, the approach is most effective when the two files being linked have a number of fields in common. In the new landscape of big data, there is a greater need to link files that have few fields in common but whose noncommon fields provide additional predictive power to determine which records should be linked. In some cases, when sufficient training data can be produced, more modern machine learning techniques may be applied.
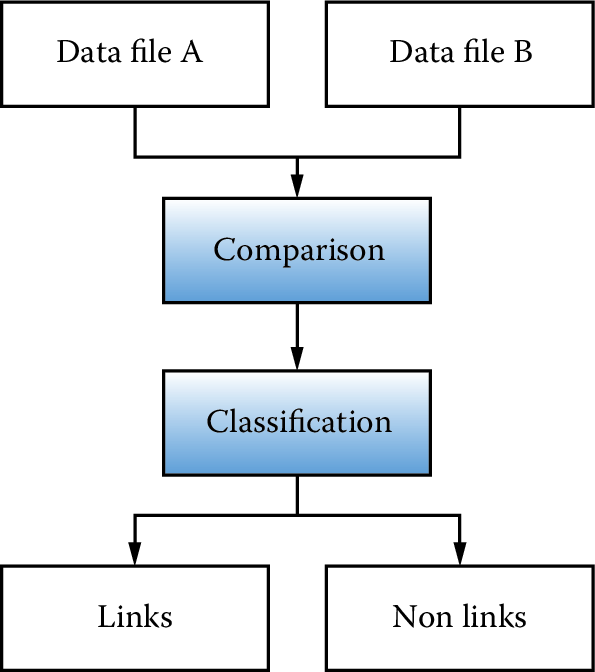
Figure 3.1: The preprocessing pipeline
The canonical record linkage workflow process is shown in Figure 3.1 for two data files, A and B. The goal is to identify all pairs of records in the two data sets that correspond to the same underlying individual. One approach is to compare all data units from file A with all units in file B and classify all of the comparison outcomes to decide whether or not the records match. In a perfect statistical world the comparison would end with a clear determination of links and nonlinks.
Alas, a perfect world does not exist, and there is likely to be noise in the variables that are common to both data sets and that will be the main identifiers for the record linkage. Although the original files A and B are the starting point, the identifiers must be preprocessed before they can be compared. Determining identifiers for the linkage and deciding on the associated cleaning steps are extremely important, as they result in a necessary reduction of the possible search space.
In the next section we begin our overview of the record linkage process with a discussion of the main steps in data preprocessing. This is followed by a section on approaches to record linkage that includes rule-based, probabilistic, and machine learning algorithms. Next we cover classification and evaluation of links, and we conclude with a discussion of data privacy in record linkage.
3.3 Preprocessing data for record linkage
As noted in the introductory chapter, all data work involves preprocessing, and data that need to be linked is no exception. Preprocessing refers to a workflow that transforms messy and noisy data into a well-defined, clearly structured, and quality-tested data set. Elsewhere in this book, we discuss general strategies for data preprocessing.18 In this section, we focus specifically on preprocessing steps relating to the choice of input fields for the record linkage algorithm. Preprocessing for any kind of a new data set is a complex and time-consuming process because it is “hands-on”: it requires judgment and cannot be effectively automated. It may be tempting to minimize this demanding work under the assumption that the record linkage algorithm will account for issues in the data, but it is difficult to overstate the value of preprocessing for record linkage quality. As Winkler notes: “In situations of reasonably high-quality data, preprocessing can yield a greater improvement in matching efficiency than string comparators and ‘optimized’ parameters. In some situations, 90% of the improvement in matching efficiency may be due to preprocessing” (Winkler 2009).
The first step in record linkage is to develop link keys, which are the record fields that will be used to estimate if there is a link between two records. These can include common identifiers like first and last name. Survey and administrative data sets may include a number of clearly identifying variables like address, birth date, and sex. Other data sets, like transaction records or social media data, often will not include address or birth date but may still include other identifying fields like occupation, a list of interests, or connections on a social network. Consider this chapter’s illustrative example of the US Patent and Trademark Office (USPTO) data (Ventura, Nugent, and Fuchs 2015):
USPTO maintains an online database of all patents issued in the United States. In addition to identifying information about the patent, the database contains each patent’s list of inventors and assignees, the companies, organizations, individuals, or government agencies to which the patent is assigned. … However, inventors and assignees in the USPTO database are not given unique identification numbers, making it difficult to track inventors and assignees across their patents or link their information to other data sources.
There are some basic precepts that are useful when considering identifying fields. The more different values a field can take, the less likely it is that two randomly chosen individuals in the population will agree on those values. Therefore, fields that exhibit a wider range of values are more powerful as link keys: names are much better link keys than sex or year of birth.
Example: Link keys in practice
“A Harvard professor has re-identified the names of more than 40 percent of a sample of anonymous participants in a high-profile DNA study, highlighting the dangers that ever greater amounts of personal data available in the Internet era could unravel personal secrets. … Of the 1,130 volunteers Sweeney and her team reviewed, about 579 provided zip code, date of birth and gender, the three key pieces of information she needs to identify anonymous people combined with information from voter rolls or other public records. Of these, Sweeney succeeded in naming 241, or 42 percent of the total. The Personal Genome Project confirmed that 97 percent of the names matched those in its database if nicknames and first name variations were included” (Tanner 2013).
Complex link keys like addresses can be broken down into components so that the components can be compared independently of one another. This way, errors due to data quality can be further isolated. For example, assigning a single comparison value to the complex fields “1600 Pennsylvania” and “160 Pennsylvania Ave” is less informative than assigning separate comparison values to the street number and street name portions of those fields. A record linkage algorithm that uses the decomposed field can make more nuanced distinctions by assigning different weights to errors in each component.
Sometimes a data set can include different variants of a field, like legal first name and nickname. In these cases match rates can be improved by including all variants of the field in the record comparison. For example, if only the first list includes both variants, and the second list has a single “first name” field that could be either a legal first name or a nickname, then match rates can be improved by comparing both variants and then keeping the better of the two comparison outcomes. It is important to remember, however, that some record linkage algorithms expect field comparisons to be somewhat independent. In our example, using the outcome from both comparisons as separate inputs into the probabilistic model we describe below may result in a higher rate of false negatives. If a record has the same value in the legal name and nickname fields, and if that value happens to agree with the first name field in the second file, then the agreement is being double-counted. By the same token, if a person in the first list has a nickname that differs significantly from their legal first name, then a comparison of that record to the corresponding record will unfairly penalize the outcome because at least one of those name comparisons will show a low level of agreement.
Preprocessing serves two purposes in record linkage. First, to correct for issues in data quality that we described above. Second, to account for the different ways that the input files were generated, which may result in the same underlying data being recorded on different scales or according to different conventions.
Once preprocessing is finished, it is possible to start linking the records in the different data sets. In the next section we describe a technique to improve the efficiency of the matching step.
3.4 Indexing and blocking
There is a practical challenge to consider when comparing the records in two files. If both files are roughly the same size, say \(100\) records in the first and \(100\) records in the second file, then there are \(10{,}000\) possible comparisons, because the number of pairs is the product of the number of records in each file. More generally, if the number of records in each file is approximately \(n\), then the total number of possible record comparisons is approximately \(n^2\). Assuming that there are no duplicate records in the input files, the proportion of record comparisons that correspond to a link is only \(1/n\). If we naively proceed with all \(n^2\) possible comparisons, the linkage algorithm will spend the bulk of its time comparing records that are not matches. Thus it is possible to speed up record linkage significantly by skipping comparisons between record pairs that are not likely to be linked.
Indexing refers to techniques that determine which of the possible comparisons will be made in a record linkage application. The most used technique for indexing is blocking. In this approach you construct a “blocking key” for each record by concatenating fields or parts of fields. Two records with identical blocking keys are said to be in the same block, and only records in the same block are compared. This technique is effective because performing an exact comparison of two blocking keys is a relatively quick operation compared to a full record comparison, which may involve multiple applications of a fuzzy string comparator.
Example: Blocking in practice
Given two lists of individuals, one might construct the blocking key by concatenating the first letter of the last name and the postal code and then “blocking” on first character of last name and postal code. This reduces the total number of comparisons by only comparing those individuals in the two files who live in the same locality and whose last names begin with the same letter.
There are important considerations when choosing the blocking key. First, the choice of blocking key creates a potential bias in the linked data because true matches that do not share the same blocking key will not be found. In the example, the blocking strategy could fail to match records for individuals whose last name changed or who moved. Second, because blocking keys are compared exactly, there is an implicit assumption that the included fields will not have typos or other data entry errors. In practice, however, the blocking fields will exhibit typos. If those typos are not uniformly distributed over the population, then there is again the possibility of bias in the linked data set19. One simple strategy for dealing with imperfect blocking keys is to implement multiple rounds of blocking and matching. After the first set of matches is produced, a new blocking strategy is deployed to search for additional matches in the remaining record pairs.
Blocking based on exact field agreements is common in practice, but there are other approaches to indexing that attempt to be more error tolerant. For example, one may use clustering algorithms to identify sets of similar records. In this approach an index key, which is analogous to the blocking key above, is generated for both data sets and then the keys are combined into a single list. A distance function must be chosen and pairwise distances computed for all keys. The clustering algorithm is then applied to the combined list, and only record pairs that are assigned to the same cluster are compared. This is a theoretically appealing approach but it has the drawback that the similarity metric has to be computed for all pairs of records. Even so, computing the similarity measure for a pair of blocking keys is likely to be cheaper than computing the full record comparison, so there is still a gain in efficiency. Whang et al. (2009) provide a nice review of indexing approaches.
In addition to reducing the computational burden of record linkage, indexing plays an important secondary role. Once implemented, the fraction of comparisons made that correspond to true links will be significantly higher. For some record linkage approaches that use an algorithm to find optimal parameters—like the probabilistic approach—having a larger ratio of matches to nonmatches will produce a better result.
3.5 Matching
The purpose of a record linkage algorithm is to examine pairs of records and make a prediction as to whether they correspond to the same underlying entity. (There are some sophisticated algorithms that examine sets of more than two records at a time (Steorts, Hall, and Fienberg 2014), but pairwise comparison remains the standard approach.) At the core of every record linkage algorithm is a function that compares two records and outputs a “score” that quantifies the similarity between those records. Mathematically, the match score is a function of the output from individual field comparisons: agreement in the first name field, agreement in the last name field, etc. Field comparisons may be binary—indicating agreement or disagreement—or they may output a range of values indicating different levels of agreement. There are a variety of methods in the statistical and computer science literature that can be used to generate a match score, including nearest-neighbor matching, regression-based matching, and propensity score matching. The probabilistic approach to record linkage defines the match score in terms of a likelihood ratio (Fellegi and Sunter 1969).
Example: Matching in practice
Long strings, such as assignee and inventor names, are susceptible to typographical errors and name variations. For example, none of Sony Corporation, Sony Corporatoin and Sony Corp. will match using simple exact matching. Similarly, David vs. Dave would not match (Ventura, Nugent, and Fuchs 2015).
Comparing fields whose values are continuous is straightforward: often one can simply take the absolute difference as the comparison value. Comparing character fields in a rigorous way is more complicated. For this purpose, different mathematical definitions of the distance between two character fields have been defined. Edit distance, for example, is defined as the minimum number of edit operations—chosen from a set of allowed operations—needed to convert one string to another. When the set of allowed edit operations is single-character insertions, deletions, and substitutions, the corresponding edit distance is also known as the Levenshtein distance. When transposition of adjacent characters is allowed in addition to those operations, the corresponding edit distance is called the Levenshtein–Damerau distance.
Edit distance is appealing because of its intuitive definition, but it is not the most efficient string distance to compute. Another standard string distance known as Jaro–Winkler distance was developed with record linkage applications in mind and is faster to compute. This is an important consideration because in a typical record linkage application most of the algorithm run time will be spent performing field comparisons. The definition of Jaro–Winkler distance is less intuitive than edit distance, but it works as expected: words with more characters in common will have a higher Jaro–Winkler value than those with fewer characters in common. The output value is normalized to fall between 0 and 1. Because of its history in record linkage applications, there are some standard variants of Jaro–Winkler distance that may be implemented in record linkage software. Some variants boost the weight given to agreement in the first few characters of the strings being compared. Others decrease the score penalty for letter substitutions that arise from common typos.
Once the field comparisons are computed, they must be combined to produce a final prediction of match status. In the following sections we describe three types of record linkage algorithms: rule-based, probabilistic, and machine learning.
3.5.1 Rule-based approaches
A natural starting place is for a data expert to create a set of ad hoc rules that determine which pairs of records should be linked. In the classical record linkage setting where the two files have a number of identifying fields in common, this is not the optimal approach. However, if there are few fields in common but each file contains auxiliary fields that may inform a linkage decision, then an ad hoc approach may be appropriate.
Example: Linking in practice
Consider the problem of linking two lists of individuals where both lists contain first name, last name, and year of birth. Here is one possible linkage rule: link all pairs of records such that
the Jaro–Winkler comparison of first names is greater than 0.9
the Jaro–Winkler comparison of last names is greater than 0.9
the first three digits of the year of birth are the same.
The result will depend on the rate of data errors in the year of birth field and typos in the name fields.
By auxiliary field we mean data fields that do not appear on both data sets, but which may nonetheless provide information about whether records should be linked. Consider a situation in which the first list includes an occupation field and the second list includes educational history. In that case one might create additional rules to eliminate matches where the education was deemed to be an unlikely fit for the occupation.
This method may be attractive if it produces a reasonable-looking set of links from intuitive rules, but there are several pitfalls. As the number of rules grows it becomes harder to understand the ways that the different rules interact to produce the final set of links. There is no notion of a threshold that can be increased or decreased depending on the tolerance for false positive and false negative errors. The rules themselves are not chosen to satisfy any kind of optimality, unlike the probabilistic and machine learning methods. Instead, they reflect the practitioner’s domain knowledge about the data sets.
3.5.2 Probabilistic record linkage
In this section we describe the probabilistic approach to record linkage, also known as the Fellegi–Sunter algorithm (Fellegi and Sunter 1969). This approach dominates in traditional record linkage applications and remains an effective and efficient way to solve the record linkage problem today.
In this section we give a somewhat formal definition of the statistical model underlying the algorithm. By understanding this model, one is better equipped to define link keys and record comparisons in an optimal way.
Example: Usefulness of probabilistic record linkage
In practice, it is typically the case that a researcher will want to combine two or more data sets containing records for the same individuals or units that possibly come from different sources. Unless the sources all contain the same unique identifiers, linkage will likely require matching on standardized text strings. Even standardized data are likely to contain small differences that preclude exact matching as in the matching example above. The Census Bureau’s Longitudinal Business Database (LBD) links establishment records from administrative and survey sources. Exact numeric identifiers do most of the heavy lifting, but mergers, acquisitions, and other actions can break these linkages. Probabilistic record linkage on company names and/or addresses is used to fix these broken linkages that bias statistics on business dynamics (Jarmin and Miranda 2002).
Let \(A\) and \(B\) be two lists of individuals whom we wish to link. The product set \(A \times B\) contains all possible pairs of records where the first element of the pair comes from \(A\) and the second element of the pair comes from \(B\). A fraction of these pairs will be matches, meaning that both records in the pair represent the same underlying individual, but the vast majority of them will be nonmatches. In other words, \(A \times B\) is the disjoint union of the set of matches \(M\) and the set of nonmatches \(U\), a fact that we denote formally by \(A \times B = M \cup U\).
Let \(\gamma\) be a vector-valued function on \(A \times B\) such that, for \(a \in A\) and \(b \in B\), \(\gamma(a, b)\) represents the outcome of a set of field comparisons between \(a\) and \(b\). For example, if both \(A\) and \(B\) contain data on individuals’ first names, last names, and cities of residence, then \(\gamma\) could be a vector of three binary values representing agreement in first name, last name, and city. In that case \(\gamma(a, b) = (1, 1, 0)\) would mean that the records \(a\) and \(b\) agree on first name and last name, but disagree on city of residence.
For this model, the comparison outcomes in \(\gamma(a, b)\) are not required to be binary, but they do have to be categorical: each component of \(\gamma(a, b)\) should take only finitely many values. This means that a continuous comparison outcome—such as output from the string comparator—has to be converted to an ordinal value representing levels of agreement. For example, one might create a three-level comparison, using one level for exact agreement, one level for approximate agreement defined as a Jaro–Winkler score greater than 0.85, and one level for nonagreement corresponding to a Jaro–Winkler score less than 0.85.
If a variable being used in the comparison has a significant number of missing values, it can help to create a comparison outcome level to indicate missingness. Consider two data sets that both have middle initial fields, and suppose that in one of the data sets the middle initial is filled in only about half of the time. When comparing records, the case where both middle initials are filled in but are not the same should be treated differently from the case where one of the middle initials is blank, because the first case provides more evidence that the records do not correspond to the same person. We handle this in the model by defining a three-level comparison for the middle initial, with levels to indicate “equal,” “not equal,” and “missing.”
Probabilistic record linkage works by weighing the probability of seeing the result \(\gamma(a, b)\) if \((a, b)\) belongs to the set of matches \(M\) against the probability of seeing the result if \((a, b)\) belongs to the set of nonmatches \(U\). Conditional on \(M\) or \(U\), the distribution of the individual comparisons defined by \(\gamma\) are assumed to be mutually independent. The parameters that define the marginal distributions of \(\gamma | M\) are called \(m\)-weights, and similarly the marginal distributions of \(\gamma | U\) are called \(u\)-weights.
In order to apply the Fellegi–Sunter method, it is necessary to choose values for these parameters, \(m\)-weights and \(u\)-weights. With labeled data—a pair of lists for which the match status is known—it is straightforward to solve for optimal values. Training data are not usually available, however, and the typical approach is to use expectation maximization to find optimal values.
We have noted that primary motivation for record linkage is to create a linked data set for analysis that will have a richer than either of the input data sets alone. A natural application is to perform a linear regression using a combination of variables from both files as predictors. With all record linkage approaches it is a challenge to understand how errors from the linkage process will manifest in the regression. Probabilistic record linkage has an advantage over rule-based and machine learning approaches in that there are theoretical results concerning coefficient bias and errors (Scheuren and Winkler 1993; Lahiri and Larsen 2005). More recently, Chipperfield and Chambers have developed an approach based on the bootstrap to account for record linkage errors when making inferences for cross-tabulated
3.5.3 Machine learning approaches to record linkage
Computer scientists have contributed extensively in parallel literature focused on linking large data sets (Christen 2012b). Their focus is on identifying potential links using approaches that are fast, adaptive, and scalable, and approaches are developed based on work in network analysis and machine learning.
While simple blocking as described in Section Indexing and Blocking is standard in Fellegi–Sunter applications, machine learning based approaches are likely to use the more sophisticated clustering approach to indexing. Indexing may also use network information to include, for example, records for individuals that have a similar place in a social graph. When linking lists of researchers, one might specify that comparisons should be made between records that share the same address, have patents in the same patent class, or have overlapping sets of coinventors. These approaches are known as semantic blocking, and the computational requirements are similar to standard blocking (Christen 2012b).
In recent years machine learning approaches20 have been applied to record Linkage. As Wick et al. (2013) note:
Entity resolution, the task of automatically determining which mentions refer to the same real-world entity, is a crucial aspect of knowledge base construction and management. However, performing entity resolution at large scales is challenging because (1) the inference algorithms must cope with unavoidable system scalability issues and (2) the search space grows exponentially in the number of mentions. Current conventional wisdom declares that performing coreference at these scales requires decomposing the problem by first solving the simpler task of entity-linking (matching a set of mentions to a known set of KB entities), and then performing entity discovery as a post-processing step (to identify new entities not present in the KB). However, we argue that this traditional approach is harmful to both entity-linking and overall coreference accuracy. Therefore, we embrace the challenge of jointly modeling entity-linking and entity discovery as a single entity resolution problem.
Figure 3.2 provides a useful comparison between classical record linkage and learning-based approaches. In machine learning there is a statistical model and an algorithm for “learning” the optimal set of parameters to use. The learning algorithm relies on a training data set. In record linkage, this would be a curated data set with true and false matches labeled as such. See (Ventura, Nugent, and Fuchs 2015) for an example and a discussion of how a training data set was created for the problem of disambiguating inventors in the USPTO database. Once optimal parameters are computed from the training data, the predictive model can be applied to unlabeled data to find new links. The quality of the training data set is critical; the model is only as good as the data it is trained on.
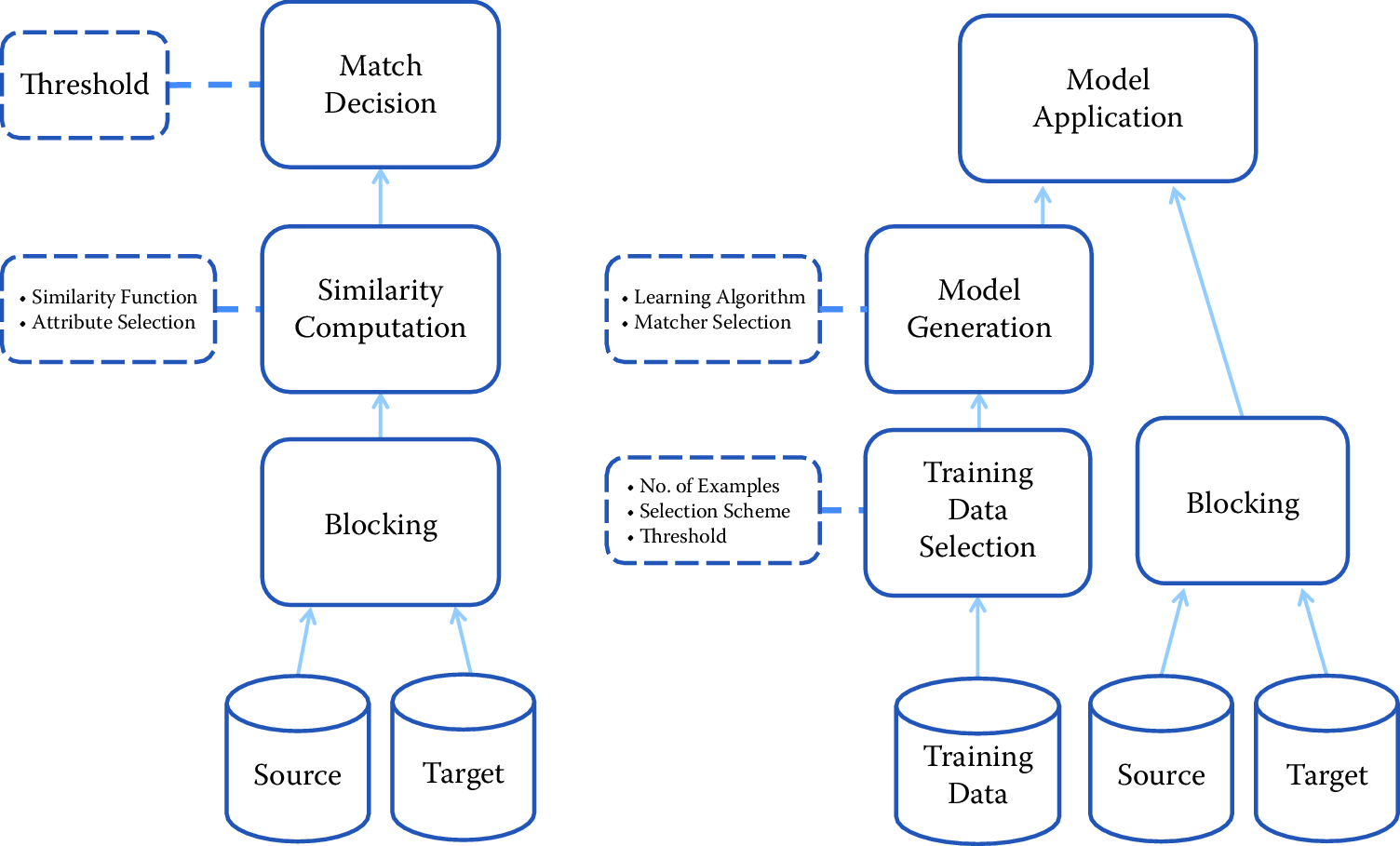
Figure 3.2: Probabilistic (left) vs. machine learning (right) approaches to linking. Source: Köpcke, Thor, and Rahm (2010)
As shown in Figure 3.2, a major difference between probabilistic and machine learning approaches is the need for labeled training data to implement the latter approach. Usually training data are created through a painstaking process of clerical review. After an initial round of record linkage, a sample of record pairs that are not clearly matches or nonmatches is given to a research assistant who makes the final determination. In some cases it is possible to create training data by automated means. For example, when there is a subset of the complete data that contains strongly identifying fields. Suppose that both of the candidate lists contain name and date of birth fields and that in the first list the date of birth data are complete, but in the second list only about 10% of records contain date of birth. For reasonably sized lists, name and date of birth together will be a nearly unique identifier. It is then possible to perform probabilistic record linkage on the subset of records with date of birth and be confident that the error rates would be small. If the subset of records with date of birth is representative of the complete data set, then the output from the probabilistic record linkage can be used as “truth” data.
Given a quality training data set, machine learning approaches may have advantages over probabilistic record linkage. There are many published studies on the effectiveness of random forests and other machine learning algorithms for record linkage. Christen and Ahmed et al. provide some pointers (Christen 2012a; Elmagarmid, Ipeirotis, and Verykios 2007).
3.5.4 Disambiguating networks
The problem of disambiguating entities in a network is closely related to record linkage: in both cases the goal is to consolidate multiple records corresponding to the same entity. Rather than finding the same entity in two data sets, however, the goal in network disambiguation is to consolidate duplicate records in a network data set. By network we mean that the data set contains not only typical record fields like names and addresses but also information about how entities relate to one another: entities may be coauthors, coinventors, or simply friends in a social network.
The record linkage techniques that we have described in this chapter can be applied to disambiguate a network. To do so, one must convert the network to a form that can be used as input into a record linkage algorithm. For example, when disambiguating a social network one might define a field comparison whose output gives the fraction of friends in common between two records. Ventura et al. demonstrated the relative effectiveness of the probabilistic method and machine learning approaches to disambiguating a database of inventors in the USPTO database (Ventura, Nugent, and Fuchs 2015). Another approach is to apply clustering algorithms from the computer science literature to identify groups of records that are likely to refer to the same entity. Huang et al. (2006) have developed a successful method based on an efficient computation of distance between individuals in the network. These distances are then fed into the DBSCAN clustering algorithm to identify unique entities.
3.6 Classification
Once the match score for a pair of records has been computed using the probabilistic or random forest method, a decision has to be made whether the pair should be linked. This requires classifying the pair as either a “true” or a “false” match. In most cases, a third classification is required—sending for manual review and classification.
3.6.1 Thresholds
In the probabilistic and random forest approaches, both of which output a “match score” value, a classification is made by establishing a threshold \(T\) such that all records with a match score greater than \(T\) are declared to be links. Because of the way these algorithms are defined, the match scores are not meaningful by themselves and the threshold used for one linkage application may not be appropriate for another application. Instead, the classification threshold must be established by reviewing the model output.
Typically one creates an output file that includes pairs of records that were compared along with the match score. The file is sorted by match score and the reviewer begins to scan the file from the highest match scores to the lowest. For the highest match scores the record pairs will agree on all fields and there is usually no question about the records being linked. However, as the scores decrease the reviewer will see more record pairs whose match status is unclear (or that are clearly nonmatches) mixed in with the clear matches. There are a number of ways to proceed, depending on the resources available and the goal of the project.
Rather than set a single threshold, the reviewer may set two thresholds \(T_1 > T_2\). Record pairs with a match score greater than \(T_1\) are marked as matches and removed from further consideration. The set of record pairs with a match score between \(T_1\) and \(T_2\) are believed to contain significant numbers of matches and nonmatches. These are sent to clerical review, meaning that research assistants will make a final determination of match status. The final set of links will include clear matches with a score greater than \(T_1\) as well as the record pairs that pass clerical review. If the resources are available for this approach and the initial threshold \(T_1\) is set sufficiently high, then the resulting data set will contain a minimal number of false positive links. The collection of record pairs with match scores between \(T_1\) and \(T_2\) is sometimes referred to as the clerical review region.
The clerical review region generally contains many more pairs than the set of clear matches, and it can be expensive and time-consuming to review each pair. Therefore, a second approach is to establish tentative threshold \(T\) and send only a sample of record pairs with scores in a neighborhood of \(T\) to clerical review. This results in data on the relative numbers of true matches and true nonmatches at different score levels, as well as the characteristics of record pairs that appear at a given level. Based on the review and the relative tolerance for false positive errors and false negative errors, a final threshold \(T'\) is set such that pairs with a score greater than \(T'\) are considered to be matches.
After viewing the results of the clerical review, it may be determined that the parameters to the record linkage algorithm could be improved to create a clearer delineation between matches and nonmatches. For example, a research assistant may determine that many potential false positives appear near the tentative threshold because the current set of record linkage parameters is giving too much weight to agreement in first name. In this case the reviewer may decide to update the record linkage model to produce an improved set of match scores. The update may consist in an ad hoc adjustment of parameters, or the result of the clerical review may be used as training data and the parameter-fitting algorithm may be run again. An iterative approach like this is common when first linking two data sets because the clerical review process can improve one’s understanding of the data sets involved.
Setting the threshold value higher will reduce the number of false positives (record pairs for which a link is incorrectly predicted) while increasing the number of false negatives (record pairs that should be linked but for which a link is not predicted). The proper tradeoff between false positive and false negative error rates will depend on the particular application and the associated loss function, but there are some general concerns to keep in mind. Both types of errors create bias, which can impact the generalizability of analyses conducted on the linked data set. Consider a simple regression on the linked data that includes fields from both data sets. If the threshold is too high, then the linked data will be biased toward records with no data entry errors or missing values, and whose fields did not change over time. This set of records may not be representative of the population as a whole. If a low threshold is used, then the set of linked records will contain more pairs that are not true links and the variables measured in those records are independent of each other. Including these records in a regression amounts to adding statistical noise to the data.
3.6.2 One-to-one links
In the probabilistic and machine learning approaches to record linkage that we have described, each record pair is compared and a link is predicted independently of all other record pairs. Because of the independence of comparisons, one record in the first file may be predicted to link to multiple records in the second file. Under the assumption that each input file has been deduplicated, at most one of these predictions can correspond to a true link. For many applications it is preferable to extract a set of “best” links with the property that each record in one file links to at most one record in the second file. A set of links with this property is said to be one-to-one.
One possible definition of “best” is a set of one-to-one links such that the sum of the match scores of all included links is maximal. This is an example of what is known as the assignment problem in combinatorial optimization. In the linear case above, where we care about the sum of match scores, the problem can be solved exactly using the Hungarian algorithm (Kuhn 2005).
3.7 Record linkage and data protection
In many social science applications data sets there is no need for data to include identifying fields like names and addresses. These fields may be left out intentionally out of concern for privacy21, or they may simply be irrelevant to the research question. For record linkage, however, names and addresses are among the best possible identifiers. We describe two approaches to the problem of balancing needs for both effective record linkage and privacy.
The first approach is to establish a trusted third party or safe center. The concept of trusted third parties (TTPs) is well known in cryptography. In the case of record linkage, a third party takes a place between the data owners and the data users, and it is this third party that actually performs the linkage work. Both the data owners and data users trust the third party in the sense that it assumes responsibility for data protection (data owners) and data competence (data users) at the same time. No party other than the TTP learns about the private data of the other parties. After record linkage only the linked records are revealed, with no identifiers attached. The TTP ensures that the released linked data set cannot be relinked to any of the source data sets. Possible third parties are safe centers, which are operated by lawyers, or official trusted institutions like the US Census Bureau.
The second approach is known as privacy-preserving record linkage. The goal of this approach is to find the same individual in separate data files without revealing the identity of the individual (Clifton et al. 2006). In privacy-preserving record linkage, cryptographic procedures are used to encrypt or hash identifiers before they are shared for record linkage. Many of these procedures require exact matching of the identifiers, however, and do not tolerate any errors in the original identifiers. This leads to information loss because it is not possible to account for typos or other small variations in hashed fields. To account for this, Schnell has developed a method to calculate string similarity of encrypted fields using bloom filters (Schnell 2014; Schnell, Bachteler, and Reiher 2009).
In many countries these approaches are combined. For example, when the UK established the ADRN, the latter established the concept of trusted third parties. That third party is provided with data in which identifying fields have been hashed. This solves the challenge of trust between the different parties. Some authors argue that transparency of data use and informed consent will help to build trust. In the context of big data this is more challenging22.
3.8 Summary
Accurate record linkage is critical to creating high-quality data sets for analysis. However, outside of a few small centers for record linkage research, linking data sets historically relied on artisan approaches, particularly for parsing and cleaning data sets. As the creation and use of big data increases, so does the need for systematic record linkage. The history of record linkage is long by computer science standards, but new data challenges encourage the development of new approaches like machine learning methods, clustering algorithms, and privacy-preserving record linkage.
Record linkage stands on the boundary between statistics, information technology, and privacy. We are confident that there will continue to be exciting developments in this field in the years to come.
3.9 Resources
Out of many excellent resources on the subject, we note the following:
There is a wealth of information available on the ADRN website (Economic and Social Research Council 2016).
Winkler has a series of high-quality survey articles (Winkler 2014).
The German Record Linkage Center is a resource for research, software, and ongoing conference activities (Schnell 2016).
The Record Linkage workbook of Chapter Workbooks provides an introduction to probabilistic record linkage with Python.23
References
Abowd, John M., John Haltiwanger, and Julia Lane. 2004. “Integrated Longitudinal Employer-Employee Data for the United States.” American Economic Review 94 (2): 224–29.
Abowd, John M., Martha Stinson, and Gary Benedetto. 2006. “Final Report to the Social Security Administration on the SIPP/SSA/IRS Public Use File Project.” Suitland, MD: Census Bureau, Longitudinal Employer-Household Dynamics Program.
Christen, Peter. 2012a. “A Survey of Indexing Techniques for Scalable Record Linkage and Deduplication.” IEEE Transactions on Knowledge and Data Engineering 24 (9). IEEE: 1537–55.
Christen, Peter. 2012b. Data Matching: Concepts and Techniques for Record Linkage, Entity Resolution, and Duplicate Detection. Springer Science & Business Media.
Clifton, Chris, Murat Kantarcioglu, AnHai Doan, Gunther Schadow, Jaideep Vaidya, Ahmed Elmagarmid, and Dan Suciu. 2006. “Privacy-Preserving Data Integration and Sharing.” In 9th Acm Sigmod Workshop on Research Issues in Data Mining and Knowledge Discovery, 19–26. ACM.
Economic and Social Research Council. 2016. “Administrative Data Research Network.”
Elmagarmid, Ahmed K., Panagiotis G. Ipeirotis, and Vassilios S. Verykios. 2007. “Duplicate Record Detection: A Survey.” IEEE Transactions on Knowledge and Data Engineering 19 (1). IEEE: 1–16.
Fellegi, Ivan P., and Alan B. Sunter. 1969. “A Theory for Record Linkage.” Journal of the American Statistical Association 64 (328). Taylor & Francis Group: 1183–1210.
Glennon, Britta. 2019. “How Do Restrictions on High-Skilled Immigration Affect Offshoring? Evidence from the H-1b Program.” http://brittaglennon.com/research/.
Herzog, Thomas N., Fritz J. Scheuren, and William E. Winkler. 2007. Data Quality and Record Linkage Techniques. Springer Science & Business Media.
Huang, Jian, Seyda Ertekin, and C. Lee Giles. 2006. “Efficient Name Disambiguation for Large-Scale Databases.” In Knowledge Discovery in Databases: PKDD 2006, 536–44. Springer.
Jarmin, Ron S., and Javier Miranda. 2002. “The Longitudinal Business Database.” Available at SSRN: https://ssrn.com/abstract=2128793.
Köpcke, Hanna, Andreas Thor, and Erhard Rahm. 2010. “Evaluation of Entity Resolution Approaches on Real-World Match Problems.” Proceedings of the VLDB Endowment 3 (1–2). VLDB Endowment: 484–93.
Kuhn, H. W. 2005. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics 52 (1). Wiley Online Library: 7–21.
Lahiri, Partha, and Michael D Larsen. 2005. “Regression Analysis with Linked Data.” Journal of the American Statistical Association 100 (469). Taylor & Francis: 222–30.
National Center for Health Statistics. 2019. “The Linkage of National Center for Health Statistics Survey Data to the National Death Index – 2015 Linked Mortality File (Lmf): Methodology Overview and Analytic Considerations.” https://www.cdc.gov/nchs/data-linkage/mortality-methods.htm.
Rodolfa, K., E. Salomon, L. Haynes, I. Mendieta, J. Larson, and R. Ghani. 2020. “Predictive Fairness to Reduce Misdemeanor Recidivism Through Social Service Interventions.” In Proceedings of the ACM Conference on Fairness, Accountability, and Transparency (ACM FAT*) 2020.
Scheuren, Fritz, and William E. Winkler. 1993. “Regression Analysis of Data Files That Are Computer Matched.” Survey Methodology 19 (1): 39–58.
Schnell, Rainer. 2014. “An Efficient Privacy-Preserving Record Linkage Technique for Administrative Data and Censuses.” Statistical Journal of the IAOS 30: 263–70.
Schnell, Rainer. 2016. “German Record Linkage Center.”
Schnell, Rainer, Tobias Bachteler, and Jörg Reiher. 2009. “Privacy-Preserving Record Linkage Using Bloom Filters.” BMC Medical Informatics and Decision Making 9 (1). BioMed Central Ltd: 41.
Steorts, Rebecca C, Rob Hall, and Stephen E Fienberg. 2014. “SMERED: A Bayesian Approach to Graphical Record Linkage and de-Duplication.” https://arxiv.org/abs/1312.4645.
Tanner, Adam. 2013. “Harvard Professor Re-Identifies Anonymous Volunteers in DNA Study.” Forbes, http://www.forbes.com/sites/adamtanner/2013/04/25/harvard-professor-re-identifies-anonymous-volunteers-in-dna-study/#6cc7f6b43e39.
Ventura, Samuel L., Rebecca Nugent, and Erica R. H. Fuchs. 2015. “Seeing the Non-Stars:(Some) Sources of Bias in Past Disambiguation Approaches and a New Public Tool Leveraging Labeled Records.” Research Policy. Elsevier.
Whang, Steven Euijong, David Menestrina, Georgia Koutrika, Martin Theobald, and Hector Garcia-Molina. 2009. “Entity Resolution with Iterative Blocking.” In Proceedings of the 2009 Acm Sigmod International Conference on Management of Data, 219–32. ACM.
Wick, Michael, Sameer Singh, Harshal Pandya, and Andrew McCallum. 2013. “A Joint Model for Discovering and Linking Entities.” In Proceedings of the 2013 Workshop on Automated Knowledge Base Construction, 67–72. ACM.
Winkler, William E. 2009. “Record Linkage.” In Handbook of Statistics 29a, Sample Surveys: Design, Methods and Applications, edited by Danny Pfeffermann and C. R. Rao, 351–80. Elsevier.
Winkler, William E. 2014. “Matching and Record Linkage.” Wiley Interdisciplinary Reviews: Computational Statistics 6 (5). John Wiley & Sons, Inc.: 313–25.
Zolas, Nikolas, Nathan Goldschlag, Ron Jarmin, Paula Stephan, Jason Owen-Smith, Rebecca F Rosen, Barbara McFadden Allen, Bruce A Weinberg, and Julia Lane. 2015. “Wrapping It up in a Person: Examining Employment and Earnings Outcomes for Ph.D. Recipients.” Science 350 (6266). American Association for the Advancement of Science: 1367–71.
Other names associated with record linkage are entity disambiguation, entity resolution, co-reference resolution, matching, and data fusion, meaning that records which are linked or co-referent can be thought of as corresponding to the same underlying entity. The number of names is reflective of a vast literature in social science, statistics, computer science, and information sciences.↩
If you have examples from your own research using the methods we describe in this chapter, please submit a link to the paper (and/or code) here: https://textbook.coleridgeinitiative.org/submitexamples↩
“Administrative data” typically refers to data generated by the administration of a government program, as distinct from deliberate survey collection.↩
This topic is discussed in more detail in Chapter Data Quality and Inference Errors.↩
This topic (quality of data, preprocessing issues) is discussed in more detail in Chapter Introduction.↩
This topic is discussed in more detail in Chapter Data Quality and Inference Errors.↩
This topic is discussed in more detail in Chapter Machine Learning.↩
See Chapter Privacy and Confidentiality.↩
This topic is discussed in more detail in Chapter Privacy and Confidentiality.↩